When Alessandro Malaspina took pendulums around the Pacific to measure gravity, he used a very simple technique. One of his officers counted pendulum oscillations and another told him when an hour had elapsed. Unfortunately, such a method could only give the time to the nearest second, and the relationship between the period T and gravity g, for a pendulum of fixed length L, which is that
T2 = π2.L/g
implies that a percent error p in the measurement of T will produce a percent error 2p in the value of gravity. Malaspina, working to the nearest second in an hour, could not hope to achieve results accurate to better than one part in eighteen hundred. This was just about adequate for confirming the generally ellipsoidal shape of the Earth, over which gravity varies by about one part in two hundred, but hopeless as a means of defining the ellipsoid parameters. For that, something much better was needed, and in England the method of coincidences was developed during the early years of the Nineteenth Century and was capable of achieving accuracies of the order of ten parts in a million, or 10 milligal in common geophysical parlance. That was enough for some serious geodetic work to be done, but when Louis de Freycinet took his four pendulums around the world, that was not the method he adopted. As he explained in the Observations du Pendule:
The nature of the stations located on deserted coasts, chosen in advance to be the theatre of our observations, led to it being decided that we would not carry an astronomical clock: from then on the use of coincidences in the experiments of the pendulum was denied us. We made up for it by the following means. As I have I said, among the instruments intended for the expedition was an astronomical counter whose pendulum could be lengthened or shortened at will: one could therefore establish a perfect synchronism between the oscillations of its pendulum and those of the [fixed-length] pendulum. A preliminary observation revealed the height at which the disc should be placed; but once this point has been found for each of the pendulums, it was easy to return to it with the help of markers, without resorting to further trial and error.
Effectively, then, the basis of the Freycinet method was the transfer of the period of the fixed-length pendulum, which ceased to be observable after a few hours, to another pendulum (the counter pendulum) which could then be compared with astronomically calibrated chronometers over a much longer time interval. It involved observing the oscillations of the fixed-length pendulum and the counter pendulum for a sufficiently long time for adjustments to be made to the latter so that the two were beating at exactly the same rate. The advantage of this system was that it was not necessary to think in terms of full completed oscillations. If the two pendulums were not synchronised, that fact would quickly become obvious. The disadvantage was that it involved a second pendulum in the process, although, admittedly, it was one that could be observed for as long as was thought necessary, because its motion would be being maintained by some form of escapement mechanism. In Freycinet’s Observations du Pendule, it is the comparison between the oscillations of this pendulum and the times recorded by the mechanical chronometers that are tabulated.

Figure 1. Table of the results of the comparison of the ‘astronomical counter’ with the chronometers, from p. 72 of the ‘Observations du pendule’. The operation appears to have been standardised on time intervals of forty minutes (24,000 seconds) as measured by Berthoud chronometer No 72. As shown in Figure 2, the other chronometers recorded slightly different numbers of seconds, while the number of beats of the counter in the same time interval (Column 5) was very different because that had been synchronised with the beating of the primary observational instrument, the fixed-length pendulum.
One of the difficulties encountered in understanding reports of scientific measurements from previous eras is that although the ‘cutting edge’ science that was being done was often described in great detail, it was seldom thought necessary to describe the more routine aspects of the work, presumably because the readers were expected to know those already. In the present case, Freycinet obviously felt no need to explain the difference between an astronomical clock and an astronomical counter, but to a modern reader they sound identical. Both had pendulums with adjustable effective lengths, and the inclusion of the word ‘astronomical’ in both names suggests that they would have been calibrated astronomically in similar ways. Column 5 of Figure 1 also strongly suggests that, rather than merely counting seconds, the counter showed times in hours, minutes and seconds. It thus seems that the only practical difference between the counter and a clock was that construction of the counter did not allow its pendulum to be viewed in a way that would allow the method of coincidences to be used.
It is very hard to work out from Figure 1 what was actually being recorded, but the situation can be clarified by converting all the times to seconds, and then replacing them by the number of seconds that have elapsed since the previous entry. This gives the tabulation shown in Figure 2.
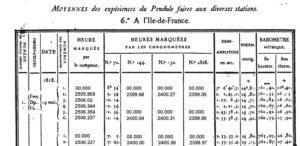
Figure 2. The equivalents of Columns 5, 6, 7, 8 and 9 of the tabulation in Figure 1, with the times converted into seconds
A remarkable feature of this tabulation is that times in seconds are being recorded to two, and sometimes three, places of decimals. At one point Freycinet describes a method used to estimate tenths of pendulum swings, but values expressed to any greater degree of precision are usually the results of averaging over a number of determinations. The tabulations, however, show that each group of observations was obtained in a continuous sequence, and it seems probable that, at least as far as the counter was concerned, the apparent high precision was introduced when corrections were made for such things as amplitude of swing, temperature and atmospheric pressure. Chronometer times are recorded only to hundredths of a second and although this is unrealistic, it might have been felt that something better than one-tenth of a second accuracy was achievable. How this could have been possible with four chronometers which should, for the readings to have any validity, have been read simultaneously, when there were only three observers (in this case, Freycinet, Duperrey and Fabré) is another unsolved mystery.
What the tabulations do not, and cannot, show, is the first stage in the experiment, in which the oscillations of the pendulum of the astronomical counter were adjusted to be exactly in phase (or at least, to have exactly the same period) as the fixed-length pendulum. This was a purely qualitative operation, and the description given by Freycinet only makes scientific sense if that is understood.
…… the pendulum and the counter being set in motion simultaneously, the only inspection of the hands of the latter, at the beginning and at the end of the experiment, made known the number of oscillations of the pendulum in the interval marked by the chronometers. All the care of the observer therefore consisted in maintaining the synchronism, which presented no difficulty, since, if one found in the long run that the counter went a little too fast or a little too slow, one could, without stopping the movements of the pendulum, delay or accelerate it by hand.
The ‘pendulum’ referred to here is clearly the fixed-length pendulum, determination of the period of which was the ultimate object of the experiment, and the ‘it’ in the last sentence, the thing that was going to be adjusted by hand, was the effective length, and therefore the period of oscillation, of the pendulum of the astronomical counter. How this could be done without necessitating a restart from scratch of the whole experiment is yet another mystery. Presumably, after the first set up (which may have been done in Toulon, or even Paris) the adjustments needed would be small, since gravity would affect both pendulums equally, but some would be necessary.
The tabulation in Figure 1 shows the results obtained on Mauritius in the short first run that extended over a mere six consecutive 40-minute intervals. There were seven other groups of observations, consisting of 8, 9 or 10 intervals each, each group being measured on a different day. The experiment thus lasted for a week and a day, and therefore occupied only a small part of the two and a half months during which the expedition was on the island, but would have been more than half the duration of the stay at Shark Bay. In fact we know from the diaries of some of the people involved that observations were made on four days at the most, towards the end of the stay. A reluctance to stay any longer may have been one of the reasons why Freycinet decided not to use the pendulums at Shark Bay, but it does not seem an adequate one. In the Falklands usable results were obtained in a single day, using only Chronometer No 72. The Louis de Freycinet who made those readings was evidently made of sterner stuff than his former self at Shark Bay. In one of the notebooks containing magnetic readings that was discovered by Sylvie Brassard in the Archives Nationales in Paris, that earlier self complained that ‘the difficulty of seeing well with eyes full of sand and covered in flies renders these observations a little unreliable (Figure 3).
Figure 3. Extract from one of Freycinet’s notebooks of magnetic results obtained in Shark Bay, catalogued in the Archives Nationales in Paris under Cataloque No. mar5jj68.
Is it possible that, after having come so far to measure gravity with his pendulums, at Shark Bay Freycinet was so deterred by the great Australian bush fly that he decided to not even attempt to do so? If so, it was an extraordinary decision, and casts considerable doubt on the reality of his commitment to science.
