When I was writing ‘The Hunt for Earth Gravity’, I had to make an early decision about what units to use. Given the situation today as far as gravity units are concerned, even geophysicists have been known to become confused, and the book would, I hoped, be read not only by professionals but by normal people. And normal people (and geophysicists) do not like fiddling about with complications like m.s-2, and still less when Greek letters begin to be involved, as in μm.s-2. That I would end up using the milligal was pretty well inevitable, because it does trip easily off the tongue. Still less forgivable from the purists’ point of view would have been the fact that I wrote it out lin full, instead of using the correct abbreviation mGal. I did put a little apology to them in the introductory pages, but in my opinion it is the purists who are to blame for the fact that a decision was needed at all..
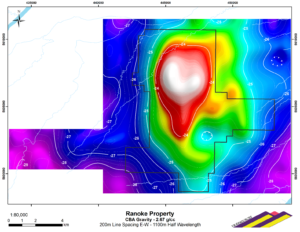
Anomaly recorded in a 2019 airborne gravity survey by Sander Geophysics Ltd for VR Resources over the Ranoke copper-gold property in norther Ontario. The contour interval is one milligal and the reduction density is stated in terms of the supposedly obsolete c.g.s units. Fortunately this at least is not a problem, The units, of grams per c.c., could equally well have been Mega-grams per cubic metre without changing the numerical value.
More than a hundred years ago physicists realised that all the units they were using, for all sorts of things, could be expressed simply in terms of mass, length and time (and one electromagnetic quantity, although they were unable to agree on what that should be). At first they didn’t do much about this, and continued to think up new names for units whenever there seemed to be a need, and the units concerned were generally rooted in the c.g.s. (centimetre-gram-second) system. Then, in the 1960s, in came the Système International (S.I,) and everything had to be based on kilogrammes, metres and seconds (and Henrys, or something like them). Out went dynes and bars, in came Newtons and Pascals, and in also came a much more rigid division between quantities that were considered fundamental (mass, length, etc.) and those that were merely derived (velocity, acceleration, etc.). Some of the advocates of change went further. They didn’t want Newtons and Pascals at all, they wanted everything to be expressed in m, kg and s.
This was not a view they were able to get adopted in fields where a lot of people were working, but relatively few people work with gravity, so there the fanatics were, in one way, successful. The Gal, the basic unit in the old c.g.s, system, was supposedly consigned to history, but the new unit, the metre per second per second or m.s-2, was never thought to deserve a name to itself. And this, I would claim, caused a problem that we have been living with ever since. The milligal has survived, and a quick internet search suggests that the results of more than half of all recent gravity surveys are being reported using it , Moreover, as the caption to the map of the Ranoke surveys hows, it has contributed to the survival of other c.g.s units. How has it managed this, when editors of physics journals have been doing their utmost to obliterate all reference to c.g.s.units for the last fifty years?
One thing the m.s-2 has in common with the Gal is that it is far too large for practical gravity work. In fact, it is even worse than the Gal, being 100 times larger. The milligal was liked because it was practical. Except in the most accurate of accurate work, one mGal was about the smallest usable contour interval, and the Earth’s field was equal to 981,000 mGal which, beingy close to a million milligals, was very easy to remember. In the S.I. system the Earth’s field was an unmemorable 9.81 m.s-2.and the practical unit for gravity survey (remembering that in the S.I. system sub-units must increase or decrease by factors of 10 cubed) had to be the μm.s-2, equal to a tenth of a milligal. No-one was going to want to type that out, or talk about micrometres per second per second, if they could help it..
One rather pathetic attempt was made to save the situation. People started referring to the μm.s-2 as the gravity unit, or g.u. No-one liked that very much. The natural response when ‘gravity units’ were mentioned was ‘which gravity units?’. It did not catch on, and so the mGal continued on its way until even journal editors no longer tried to stop it being used.
There is a further complication. Einstein was not the first of a long line of scientists to point out that gravity fields can be expressed in the same units as acceleration, although he may well have been the first to provide some sort of theoretical framework for this equivalence . The equivalence of gravity fields and accelerations was a fundamental element in his development of both special and general relativity. There are, however, people who ignore this and claim that, to maintain the analogy with magnetic fields, the basic unit of gravity field should actually be the Newton per kilogram. The dimensions are the same (LT-2), the numerical values would be the same, but the view being taken of physics would be a little bit different.
Or, a name could be selected for the unit itself, and thereafter no-one would care.
It might not yet be too late. The gravity community could still get together to rechristen the m.s-2. Galileo obviously deserved his memorial, but he has had a good innings and there are other deserving cases. Kepler, for instance. The nanoKep has a nice chunky feeling, even if it would represent a unit a little bit smaller than our most ambitious efforts at field measurement. Who knows, it might catch on!
The adoption of the Kepler could have another consequence, that would be welcomed, surely, by all those working in gravity gradiometry, because there IS a unit for gravity gradient, and it is a real pain to type . Named after one of Hungary’s most famous scientists, it is the Eötvös. All those damn dots, that have you hunting all through the symbol libraries if you do not have a keyboard from one of the countries where the ö is in common use. And even when you have got past that hurdle, the definition of the unit seems to make no sense. Why should it be a gradient of 1 mGal per ten kilometres, as is so commonly stated.?
The reason (which is not so commonly stated) is that, unlike the mGal, the Eötvös belongs in the S.I. system. It is actually one billionth of a m.s-2 per metre, but since so few people use the m.s-2, that fact is quite well hidden.
Is there anyone out there in the FTG community in favour of the nanoKep per metre? And getting rid of those ‘o’s with their damned dots?
