In ‘The Hunt for Earth Gravity’ I wrote about Maskelyne’s attempt to ‘weigh the Earth’ on the inhospitable slopes of Schiehallion in 1775, and also Cavendish’s efforts to do the same thing in his house on Clapham Common twenty years later. The two came up with rather different results. Charles Hutton (to whom Maskelyne left the boring bit of doing the calculations) decided that the mean density of the Earth must be about four and a half times the density of water, whereas Cavendish concluded it was 5.48 times that of water, a difference that was, he stated, “rather more than I should have expected”. His own estimate of 5480 kg.m-3 was quite remarkably close to the modern estimate of 5515 kg.m-3.
Given the discrepancy between the two 18th Century estimates, it is not surprising that someone in the 19th Century should try to resolve the conflict, and after another twenty years had passed, the young George Biddel Airy (the Airy of isostasy fame, but many years before he produced the theory that bears his name) decided to make the attempt, by measuring gravity at depth in a mine and also on the surface immediately above the underground station. His first attempts, in 1824 and 1826 in conjunction with William Whewell, was made in the deep Dolcoath tin-copper mine in Cornwall and ended inconclusively, thanks to two disasters that had nothing directly to do with the experiment and everything to do with the intransigent nature of Cornish mines and miners. A result of sorts was obtained, but, at seventeen times the density of water, was too far from the two other efforts to be considered a serious contribution.

George Biddel Airy.(27 July 1801 – 2 January 1892) Image Wikipedia commons
The failure at Dolcoath must have rankled, because thirty years later Airyreturned to the task. In trying again, this time in a Yorkshire coal mine, the Harton colliery near South Shields. He did not himself take part in the actual observations (rounding up six younger men to do that for him) but was clearly determined that this time the result should be definitive. Having decided that he would still use fixed length ‘invariable’ pendulums timed against pendulum clocks using the ‘coincidence’ method (and, in fact, he did not have many other options), he went to great lengths to ensure that all the necessary corrections were made with the greatest possible accuracy.
He would use electrical signalling, only recently available, to inter-relate the clock in the mine to the clock at the surface, rather than the spring-chronometers that he blamed for the failure in Cornwall.
He would use his available manpower to make the operation almost continuous, over a period of almost three weeks.
He would make all the standard corrections, beginning with the correction for the finite arc of swing.
And continuing with the correction for the effect of temperature on the lengths of the various pendulums involved
And the correction for the density of the atmosphere
All these corrections were made with meticulous attention to detail and with calculations extending over pages and pages of text, because he believed that “the mere determination of the relative rates of the detached pendulum and the clock pendulum, by the method of coincidences, is accurate almost beyond conception. I do not see how it is possible that an error of 0.01 seconds per day can enter from this cause.” Not content, however, with his initial results, he carried out a further set of experiments once the instruments were back in London, to check the accuracy of his temperature corrections, and made some small adjustments on the basis of what he discovered. Then, and finally, he added as an addendum some further calculations by George Stokes which took account of the ellipticity of the Earth.

The Harton colliery in the 19th Century. Royal Astronomical Society / Science Photo Library
All of these calculations had to be made by hand, laboriously, using tables of eight-figure logarithms, and yet, at the end, all that had been estimated was the difference in the gravity field at the two stations. To turn that into an estimate of the mean density of the Earth, still further work had to be done, and here it is necessary to give some thought to the mathematics of the colliery experiment.
Should gravity increase or decrease when going down a mine? Airy began his discussion of this question by pointing out that “the attraction of the spherical shell upon a point at or within its inner surface is nothing”, and by dividing the Earth into two parts, these being a sphere of density D, radius r, below the underground observation point, and a spherical shell of density d and thickness c between the underground and surface observation points. Rather than going into the mathematics, it is worth considering these two effects qualitatively.
Suppose the density of the shell is the same as the mean density of the Earth. Going down the shaft takes the observer progressively closer to the centre of the spherical mass that is causing the gravitational attraction but progressively decreases that mass, because the mass of the increasingly thick shell outside the observation point ceases to have any effect on the gravity field. Since the attraction increases as the inverse square of the radius and the mass decreases as its cube, the decrease will dominate.
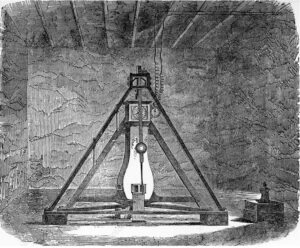
The pendulum apparatus in the Harton Colliery. Royal Astronomical Society / Science Photo Library
If, on the other hand, the shell has zero density, then the gravitating mass is constant and the only effect of the decreasing radius would be to increase the attraction in accordance with the inverse square rule. It is therefore clear that whether gravity increases or decreases depends on the density of the shell, which can be assumed to lie somewhere between zero and the mean density of the Earth, and that there will be an intermediate value for which the gravity field would not change during the descent into the mine. The calculations are relatively straightforward and show that if the density of the shell is two-thirds of the mean density of the sphere, gravity will remain constant while descending the shaft. Since in practice it is always less than this value, gravity increases, but it is also clear that the accuracy of the estimate of the mean density of the Earth depends on the accuracy of the estimate of the gravity effect of the shell. This, in effect, is where Maskelyne failed. He measured the ratio of the gravity effect of the Earth to the gravity effect of nearby topographic masses with great precision. The error in his final value for Earth density was due almost entirely to the error in estimating the gravity effect of the topography. Airy, in his experiment, had to be more accurate in estimating the gravity effect of the shell.
He went about it with the same attention to detail that he had applied to the pendulum measurements. The measurement of the height difference between the two stations was essentially a trivial operation but he was meticulous when it came to having it done. The more difficult question of the shell density was solved by enlisting the help of the colliery, obtaining samples of rock all the way down the shaft, and having their densities measured. A part of his tabulation of the results is shown in Figure 3. It is hard to fault it for dedication. From the results he concluded that his shell consisted of 1211 feet of rocky and shaly beds; specific gravity 2.56, 30 feet of coaly beds, specific gravity 1.43 and 15 feet completely worked out, specific gravity 0, and that its mean specific gravity was 2.50.

A part of Airy’s log of the strata in the Harton Colliery, from his report to the Royal Society
Finally, Airy persuaded the Mayor and Corporation of South Shields to commission a new topographic survey, from which he laboriously calculated the terrain corrections.
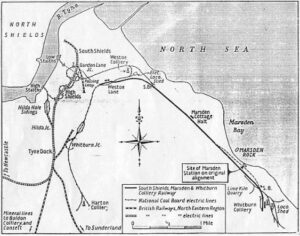
Location map of the Harton colliery
There is no doubt that this second attempt by Airy was a very serious one. It had involved liaising with a multitude of different people and immense labour in calculation. It must also have involved very considerable expense. It would be nice to be able to record that all this effort had been worthwhile, and Airy, although he expressed himself rather modestly, had little doubt that it had been. “I shall” he wrote “content myself with expressing my opinion, that the value now presented is entitled to compete with the others, on, at least, equal terms”.
Expressed in SI units, the value presented was 6565 kg.m-3. It was in error by almost 20%. Where did Airy go wrong?
That is a matter for a future blog
