Extreme gravity
Extremes are now again in fashion. Extreme runners scorn the trivialities of the marathon, which lasts only a few hours, in favour of running for days across the Sahara. Extreme cyclists cross Siberia and extreme climbers ignore the most basic of aids in scaling verrtical cliff faces. In biology the study of extremophiles, organisms that can survive where no sensible life form would wish to live, is the current hottest of hot topics. But – extreme gravity? Is there anything to be gained by searching for those points on the Earth’s surface where gravity is highest, lowest, steepest? Possibly, because extremes always have the potential to challenge preconceptions.
First, of course, the sort of gravity being considered has to be defined. Is it raw ‘absolute gravity’, the actual strength of the Earth’s gravity field? That is a big number, almost a million, if stated in milligals, but it is affected by several different things and, to make geological sense of it all, corrections have to be applied. Correcting for the effect of an ideal Earth (the latitude correction) produces a much smaller number, which is in many cases largely determined by the height of the measuring point above the surface of that ideal Earth. Or below it, but the additional complexities of correcting marine gravity are not going to be considered here. This simplest correction takes account of height and nothing else. It is called the free-air correction, and produces a different ‘gravity’, the free-air gravity.
That, however, is not the end of it, because there is normally not air but rock of some sort between the measuring point and the ideal surface of the ideal Earth. The correction can be calculated by many different routes: crudely, by replacing the actual mountains and valleys by a uniform flat plate extending on all sides to infinity, or in more complicated ways by taking account of the actual shapes of the mountains and valleys, by allowing for the curvature of the Earth, and by assuming different densities for the rocks in different places. At its simplest we have simple Bouguer gravity, while the more complicated approaches produce other things, which may be called the ‘extended’ or ‘complete’ Bouguer gravity (or something else again).
And yet the process is still not finished, because most mountains have deep roots, immersed in a heavier but weaker surrounding medium (the mantle). This is isostasy, and the isostatic roots decrease gravity in the vicinity of high mountains. How this occurs in any particular place is never known exactly, so the calculation uses models, and for each model there is a different version of what is called the ‘isostatic correction’. And when that is applied, on top of all the others, it produces the ‘isostatic anomaly’.
Enough is enough. Back to the beginning. Where on Earth, on its land surface, would the highest absolute gravity be measured?
It should be relatively easy to guess, at least approximately. All that is necessary is to find the bit of land closest to the centre of the Earth, and because the Earth’s polar radius is less than its equatorial radius, that will be at sea level on the piece of land closest to one of the poles.
But the solution is not so easy, because the Earth’s two poles have very different topographies. What they have in common is that those topographies are very hard to get to. The North Pole is out in the Arctic Ocean, and the nearest bit of dry land is the northern tip of Greenland, at about 83.65°N. Difficult, but possible, because for some of the year it is now ice-free. The South Pole presents a much bigger problem, and it is a problem of definition as much as anything else, because it is a place where the land surface is only a few hundred metres above sea level, but is covered by some 2700 metres of ice. Ice having only about one-third of the density of standard continental crust, the downward pull of that great slab is really quite small, and comes nowhere near to compensating for the extra height. Whatever the absolute gravity on the hidden land surface, the absolute gravity on the ice surface above it will be about 730 mGal less.
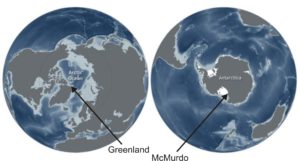
The ‘highest absolute gravity’ candidates. Base from NOAA climate.gov.
That gives the North Pole the crown. If the definition demands a site where solid rock is actually exposed, and at very low altitude, then the best the Antarctic can offer is the dry valleys near McMurdo sound, but they are all much further from their pole than the northern tip of Greenland is from its. Greenland wins, and at its northernmost point the theoretical or ‘normal’ gravity is about 983,150 mGal. There is no reason to suppose that the actual absolute gravity is very different.
Locating the place with the lowest absolute gravity should, in principle, be much simpler, and at least it does not involve an argument about definitions. It is also provides quite a good question for testing students who are just trying to get to grips with gravity corrections. The right place should be the place that is furthest from the centre of the Earth, and that means the top of a high mountain close to the equator. There is a certain amount of trade-off to be made, of height against latitude, but, by common consent the point in question is at the top of Chimborazo, at 6310 metres above sea level. And, gravitationally, there is another factor favouring low absolute gravity. The Andes are underlain by a deep isostatic gravity low, which must further reduce the absolute gravity at the summit. There is just one nagging doubt.
Measured from sea level, the summit of Chimborazo is about 2500m lower than the summit of Everest. It is the polar flattening of the Earth that gives Chimborazo the advantage, but shouldn’t the extra elevation, which in free air would produce a decrease about 750 milligal, make a difference? And isn’t Everest underlain by a truly gigantic isostatic gravity low?
These things have to be considered, but the isostatic case is a very weak one, because the isostatic low is associated not primarily with the Himalayas but with the Tibetan Plateau, and the plateau is the place where the extreme values are reached. The isostatic effect at Everest, at the plateau edge, is not enormously greater than the isostatic effect at Chimborazo. At the Everest Base Camp, the Bouguer gravity, a proxy for the isostatic effect, has been estimated at -327 mGal.

The ‘lumpy’ Chimborazo and the pointed Everest (photos American Alpine Institute and Trip Advisor).
Nor is the elevation case much stronger. On both summits the measurement would be made on rock, not in the free air, and although Everest is a much more pointed mountain than Chimborazo, and the terrain effect at its peak is likely to be much greater, it could scarcely be greater by much more than a couple of hundred milligal . Not nearly enough to counteract the more than 1100 mGal difference in theoretical sea level gravity between the latitudes of the two mountains.
At the latitude of Chimborazo, that theoretical gravity is 978,035 mGal.
And the actual absolute gravity at its summit?
It is not, I am told, a difficult climb, even carrying a gravity meter. It’s time someone went up and found out.
